Efficient Design of Majority-Logic-Based Approximate Arithmetic Circuits using Quantam-Dot Celluar Automata (QCA) Technique

Abstract

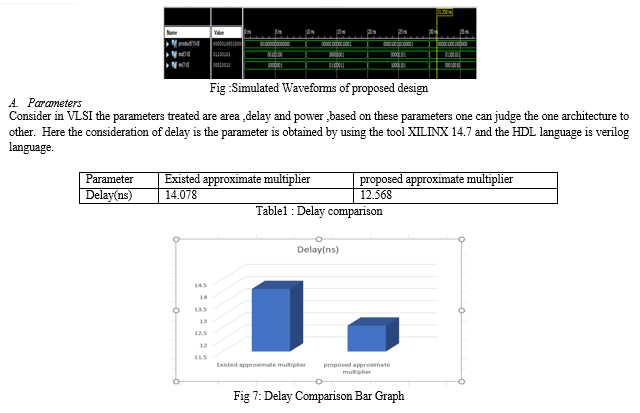
In this paper, we propose an approximate multiplier that is Approximate computing (AC) offers benefits by reducing the requirement for accuracy, thereby reducing delay. The majority logic (ML) gate functions as the fundamental logic block of many emerging nanotechnologies. These adders are designed to prevent the propagation of inexact carry-out signals to higher order computing parts to enhance accuracy. We implemented the proposed multiplier by using a unique partial product reduction (PPR) circuitry, which was based on the parallel approximate 6:3 compressor. The implemented by quantum-dot cellular automata (QCA) are analyzed to evaluate the adder designs. A significant improvement is observed over previous designs based on the experimental results. The proposed design is further designed using kogge stone adder. Finally, It has added advantage that reduces logic size and facilitates with less power and delay. Here we are using Verilog HDL and Xilinx ISE14.8 software tools for simulation and synthesis purpose.

Introduction

I. INTRODUCTION

With the increasing integration of circuits, the traditional CMOS technologies have been gradually limited in the design of VLSI circuits. The power dissipation of  computing systems is still an increasingly serious problem, despite advances in semiconductor technology and energy-efficient design techniques [1]. As a new computing paradigm at the nano scale, approximate computing (AC) offers a promising solution to the VLSI industry by trading precision for reduced complexity and power consumption. AC takes advantage of the inherent error tolerance of the application to balance performance and accuracy of the circuit [2]. As a result, AC can be applied to many applications and architectures, such as data analysis, image recognition, multimedia, and signal processing [3], [4]. There have been a number of emerging nanotechnologies proposed in recent years, including quantum-dot c ellular automata (QCA) [5], nano magnets logic [6], and spin-wave devices [7]. These techniques are based on the majority logic (ML) abstraction, which differs from the traditional Boolean logic. The intrinsic energy consumption of nanotechnology is lower than that of CMOS. Also, the ML function is more expressive than these traditional two-input Boolean logic operations. Thus, this article uses ML to implement the proposed designs for approximate circuits. Adders and multipliers are arithmetic units that are widely used in computing systems. Thus the performance of computing systems is significantly influenced by the speed and power consumption of arithmetic circuits. Although researchers have proposed a variety of designs for the approximate circuit in the transistor-based technologies [8], [9], [10], these designs are less attractive when implemented in other nontransistor or technologies that use different logic gates. As an example, the design shown in [12] adopts a lot of XOR operations for carry generation and propagation. However, ML operations are inefficient when representing XOR gates with two or more inputs; for more details, see Section II-A. In this article, we propose both ML-based approximate full adders (MLAFAs) and ML-based approximate multipliers (MLAMs). These contributions are described in the following.

1. Our work presents a direct method for designing multibit approximate circuits, allowing us to reduce the critical path delay and enhance the accuracy of our proposed 2- and 4-bit adders significantly. As a result of the special structure of the proposed adders, long computation sequences are less prone to accumulating errors.
2. We propose an approximate parallel 6:3 compressor and show how it can be used in combination with the Wallace-based distinctively partial product reduction (PPR) circuitry to produce a simple and efficient 8 × 8 multiplier. As an alternative to the conventional 4:2 compressor, the proposed compressor can compress six partial products simultaneously with a simpler circuit structure.
3. Adders and multipliers are used in image processing applications. The results are evaluated by considering structural similarity (SSIM) and peak signal-to-noise ratio (PSNR). In addition, multipliers are used to develop low-power neural network (NN) accelerators for machine learning.

We conduct experiments on 8-bit MLAFAs and MLAMs with applications to image processing. The experimental results are presented in three aspects. In terms of accuracy, the maximum absolute error (MAE) and normalized mean error distance (NMED) of the proposed designs are significantly improved when compared with previous works .The proposed 8-bit approximate adder reduces MAE by 50% and NMED by 38.1%, respectively. As a result of efficient designs, the number of majority gates, inverters, and logic levels is reduced for logic implementation. In an 8-bit approximate multiplier design, the number of majority gates, inverters, and logic levels is decreased by 16.67%, 50%, and 42.86%, respectively. SSIM and PSNR are improved after evaluating the image processing designs. We found that there is one design that makes the resulting image infinitely close to the original. In terms of machine learning application, the proposed multiplier-based accelerator achieved 97.18% accuracy for LeNet-5 on the MNIST dataset. The proposed adders are implemented using the QCA technology. The results obtained by simulations performed with the QCA design tool, QCA Designer-E 2.2, that show the performance of the QCA layouts is generally consistent with the logic implementation cost. Due to the reduction in the number of majority gates, inverters, and logic levels of logic graph, the power consumption, clocking phases, and area of QCA realization are reduced.

The remainder of this article is structured as follows. In Sections II and III, the fundamentals of exact circuits, error metrics, related works, and motivation are outlined. Sections IV and V describe the proposed ML-based approximate adders and multipliers as well as the comparison with previous works, respectively. Section VI concludes this article.

II. PRELIMINARIES

A. Majority Logic

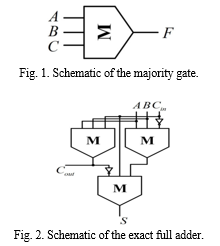
The ML operation acts as a voter, denoted as M(x1,..., xn), where n is typically an odd number. The function evaluates to true if more than [(n − 1)/2] variables are true. The logic expression of a majority-of-three function (see Fig. 1) over three Boolean variables A, B, and C is

F = M(A, B,C) = AB + AC + BC.                                                 (1)

By setting any one of the inputs to constant zero or one, the majority-of-three function is reduced to AND or OR, respectively. As an example, M(A, B, 0) = AB and M(A, B, 1) = A + B. Hence, ML can be seen as a generalization of the traditional AND/OR-based logic. Recently, the ML-based logic is established as a graph representation for synthesizing Boolean functions [23], [24], which yields promising synthesis results for both FPGA/ ASIC [25], [26] and nanocircuit designs [27], [28]. The arithmetic circuits often use XOR gates. XOR expressions with two inputs require three majority-of-three operations, which is A ⊕ B = M(A¯, M(A, B, 1), M(A, B¯, 0)).

B. ML-Based Exact Full Adder

Given three Boolean variables A, B, and carry input Cin, the carry output operation of an ML-based exact full adder

III. RELATED WORK AND MOTIVATION

A. ML-Based Approximate Adders

The CMOS-based approximate circuit designs cannot be directly applied to the ML-based circuits because of the differences in the underlying logic. Therefore, there is limited research on the design of the ML-based approximate adders [15], [16], [33], [34]. Labrado et al. [33] proposed an approximate 1-bit full adder, subtractor, as well as addition–subtraction devices, but investigations into multibit approximate adder designs are lacking. An approximate 1-bit full adder was proposed in [34], which was combined with the adder proposed in [33] to develop multibit approximate adders by cascading. In a recent study [15], multibit approximate adders are applied to image processing techniques to study the tradeoff between performance and error. In [16], two novel 2-bit approximate adders, namely, the most subadder (MSA) and the least subadder (LSA), were presented. For n-bit addition, the two most significant bits and the remaining n − 2 bits of operands are exploited separately. The MSA which consists of two exact full adders was used to generate the final carry output signal. Moreover, the LSA requires more ML gates and levels than other 2-bit adders currently available.

???????B. ML-Based Approximate Compressors

Compressors are indispensable for partial product computation in multipliers. There were several efficient 4:2 approximate compressors proposed in the literature [15], [17], [18], [19], [20], [21]. Liu et al. [15] and Angizi et al. [18] proposed several 4:2 approximate compressors by stacking techniques based on the 1-bit approximate full adder proposed in [33] and [34]. In contrast, a 4:2 approximate compressor proposed in [17] was designed based on truth table modification. To avoid the power consumption problem caused by the XOR gate, an imprecise 4:2 compressor implemented with only one majority gate was proposed in [19]. Moreover, Sabetzadeh et al. [20] and Salmanpour et al. [21] ignore Cin and Cout signals as efficient ways to improve the performance of compressors.

???????C. Motivation

Large-bit width adders designed with small-bit building adders are highly dependent on the carry chain structure of the building adders. Compressors, in contrast, play a significant role in PPR in large-bit width multipliers. Both the adders and compressors must address the propagation of erroneous carries to higher bits in the carry chain design to maintain accuracy. As a result, the primary purpose of this article is to design a carry chain structure that is efficient for building adders and compressors. In this article, the computation of the carry output of the proposed approximate adder is independent of the carry input of the previous stage. This allows for a smaller area and a lower logic depth.

A 4:2 compressor is typically used for accumulating the partial product of the multiplier in the existing works. Since adders connect compressors, the 4:2 compressor with a carry chain also has the problem of propagating erroneous carries to the higher bits. Comparatively, the 6:3 compressor is not affected by the carry chain, and it saves its unique carry output for the next compression stage. Also, this compressor is more efficient than the standard 4:2 compressor when it comes to compressing six partial products at the same time regardless of carry chain differences. As not all the six inputs of the 6:3 compressor are used simultaneously, this feature can effectively reduce the size of the multiplier by only generating the product that is required.

those of MLAFA2121 and MLAFA2133. The NMED of MLAFA-I and MLAFA-II has reduced by 23.32% and 35.12%, respectively, compared with these cascaded 4-bit approximate adders. The number of MAJ gates has improved by 16% as well. Therefore, the proposed designs significantly reduce the negative impact of incorrect carries based on both the 2- and 4-bit approximate adders. C. Application and Simulation To further validate the performance of the proposed adders, the reference 8-bit ripple-carry adders (RCAs) proposed in [15] are replaced by the proposed 8-bit approximate designs. Adders are used to combine images by adding two of the same images pixel by pixel and combining them into one single image. The SSIM and PSNR [36] of each image are used as a measure of the differences between the image processed by the approximate adder and the original image. In the case of two images, one of which is distortion-free and the other distorted, the SSIM of the two images can be viewed as a measure of the image quality of the distorted image. SSIM, which ranges from −1 to 1, measures the similarity between two images and measures one when the images are identical. The PSNR is the logarithm of the squared error between the original and processed images relative to the square of the maximum value of the signal. The unit of PSNR is decibel (dB). The higher the PSNR value, the less distortion it represents. For comparison, we use MLAFA1212-1212 [15], which achieves relative efficiency tradeoff between accuracy and the number of logic gates, as the original 8-bit RCA. Since 8-bit adders can be implemented by cascading 2- or 4-bit adders, we adopt the designs proposed in [15], [16] and ours to construct several representative 8-bit adders for comparisons.

Accuracy: With cascading larger bit-width adders, MAE and NMED for the 8-bit adders are reduced significantly. As an example, the proposed MLAFAI-I consumes the same number of majority gates and inverters, but with a logic depth of two instead of five in MLAFA1212-1212. Specifically, the MAE is reduced from 170 to 85, and the NMED is optimized from 0.0904 to 0.0560, which represents improvements of 50% and 38.1%, respectively. The reasons come from two aspects.

On one hand, the proposed larger bit-width adders are noncascaded designs, which have low MAEs inherently. It means that when the adders are used as a building block for large circuits, the resulting ED is relatively smaller than a cascaded design with several smaller bit-width adders. In contrast, the proposed adders are independent of the carry chain, so they do not cause unexpected errors resulting from previous blocks’ carries.

Logic Implementation Cost: Among the designs, MLAFA12b-bb, MLAFAbb-bb, MLAFAI-I, and MLAFAII-II have a logic depth of two, which is the minimum. This is also due to the design outputs not being dependent on the carry inputs, thus preventing the carry chain from growing on a critical path.

SSIM and PSNR: The results of SSIM and PSNR indicate that the proposed designs perform better than MLAFA12, MLAFA33, LSA, and MSA. In the most efficient hybrid design, MLAFALSALSA-LSAMSA, the SSIM and PSNR are 0.7313 and 36.9670 dB, respectively. After using our proposed designs as a building module, six designs got SSIM of more than 0.8 and seven got PSNR greater than 40 dB. For image processing, the proposed 4-bit designs generally outperform the proposed 2-bit adders, with the exception of MLAFA-b. Interestingly, as the number of MLAFA-b modules increases, the values of SSIM and PSNR are much better than the others. Also, the experiments yielded results that were almost indistinguishable from the original figure when the number of MLAFA-b modules was four. Thus, the SSIM was one and the PSNR was infinity.

Layouts: Both the proposed and compared circuits are implemented by the QCA technology, in which the ML-based gates are the building logic blocks. The circuit layouts are designed, simulated, and characterized using the QCA Designer-E 2.2 software tool with default settings. With regard to the QCA layouts, we use a multilayer wire crossing approach with a uniform layout strategy and a four-phase clocking scheme. The comparison results of the 8-bit approximate adders are shown in Table VI, in which the number of QCA cells, area, delay (the number of clocking phases), and energy are demonstrated, respectively. The design MLAFAI-I achieves the minimum number of QCA cells, minimum area, minimum delay, and minimum energy. In general, the performance of layouts is consistent with the cost of logic implementation. However, there are some exceptions due to the layout strategy adopted. As an example, the design MLAFA12b-bb, which has a logic depth of two, uses four clocking phases in QCA compared with three other designs (MLAFAbb-bb, MLAFAI-I, and MLAFAII-II). It is observed from Table VI that the proposed designs outperform the designs in [15] above all the metrics when constructing large-bit width adders. This is mainly due to the fact that the carry signals of the proposed adders are independent of the carry chain. In Fig. 6, the layouts of the proposed designs are extended in only one direction, which greatly reduces the area, delay, and energy consumption of the circuit. Although the designs proposed in [16] are likewise independent of the carry chain, their complex structural design results in slightly worse performance overall.

Small-bit width arithmetic circuits are extensively studied due to their energy efficiency. Researchers have demonstrated that NN inference computational bit width can be scaled down to just a few bits [37]. We also construct some special 16-bit adders for further evaluation in addition to the 2-, 4-, and 8-bit adders. The accuracy and QCA layout metrics are shown in Table VII. For the accuracy metrics, MAE and NMED are generated by simulating 210 × 210 × 2 combinations of input operands that are randomly created and satisfy the uniform distribution. The proposed adders still perform well when constructing adders with large-bit width. Compared with a general adder, adders with independence from the carry chain exhibit progressively larger advantages in area, delay, and power consumption as the bit width increases. When compared with MLAFAII-II-II-II, the MLAFALSALSA-LSALSALSALSA-LSAMSA design has better metrics in MAE and NMED. However, our design has a lower implementation cost in the QCA layouts.

???????C. Proposed Approximate Multipliers

A parallel 6:3 compressor and a PPR circuitry are proposed in this section that yield an efficient balance between logic implementation cost and accuracy. Then we create and use an efficient, imprecise multiplier for multiplying the images and building energy-efficient NN accelerators. A. Proposed Approximate Compressor The three steps of multiplication are: 1) partial products generation; 2) PPR; and 3) final products generation by RCA. By taking these three elements into account, PPR contributes significantly to latency, power consumption, and design complexity.

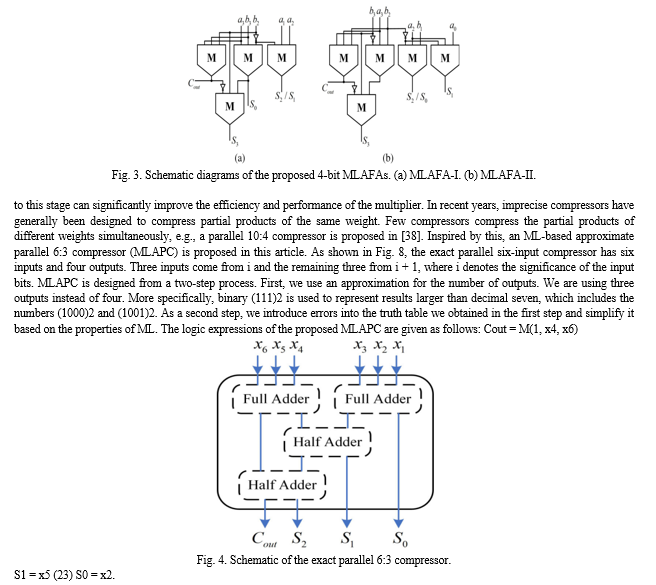
In Fig. 9, each partial product bit is represented by a dot. The reduction is done using two full adders along with 13 MLAPCs. A 7-bit RCA is then used to produce the final product. There are two possible reasons why the partial products shown by blank circles in Fig. 9 are not generated. In the proposed MLAPC, there are six inputs; however, the first and third inputs (x1 and x3) are not used, and they are not required in the production phase. Second, the outputs of the compressors are not required in the next stage. By removing the partial products indicated by the red dots in Fig. 9, additional area can be saved in the multiplier. MLAPC does not have a symmetric input, which causes the error to be determined by the order in which the partial products are connected to the inputs. As a result, the output value may change if the inputs are permuted. Therefore, the error of the PPR tree depends on the specific connections of each partial product to each input of the approximate compressor. This was ignored in previous works. Based on a uniform and independent distribution of the inputs, we assume that all the partial products are independent of each other and their probability of being “1” (as indicated simply by a probability below) is 1/4 (since inputs “00,” “01,” “10,” and “11” result in the outputs “0,” “0,” “0,” and “1,” respectively). As a result, there is no preferential connection between the partial products of the first stage and the approximate compressor inputs. However, the probability of some partial products in the second stage has changed after the first stage has been reduced by MLAPCs. The blue dots in Fig. 9 represent the partial product with a probability of 7/16. Since the accuracy of MLAPC is more influenced by Cout, it is crucial to assign the partial products with different probabilities. There are three distribution cases. 1) Case 1: The probabilities of two inputs of the Cout signal generator are both 7/16. 2) Case 2: The probabilities are 7/16 and 1/4, respectively. 3) Case 3: Both the inputs have probabilities of 1/4. As a result of practical experiments, case 3 works best in the approximate multiplier. C. Image Processing Using Approximate Multipliers We apply an unsigned 8 × 8 multiplier to validate the performance of approximate multipliers for image processing.

???????E. DADDA Multiplier

Multipliers are critical in the present advanced flag handling and for different applications. Numerous scientists have attempted and many are endeavoring to plan the multipliers which will enhance the outline parameters like – speed, low power utilization less range or mix of these in one multiplier by making them appropriate for various fast, low power VLSI usage. The basic idea of DADDA multiplier depends on the underneath framework shape appeared in Fig 7.

???????

Conclusion

In this project presents the designs, analysis a novel approximate 6:3 compressor and a unique PPR circuit are proposed for the parallel compressor in multiplier using koggestone adder. They are able to reduce the delay without significantly degrading the quality of the multiplier. In addition, the proposed compressor is strongly generalizable. It requires only one majority gate with a constant of “1,” which is an OR gate that is excellently implemented in other logic primitives. Compared with other existing approximate designs, there is a significant improvement in terms of delay.

References

[1] Q. Xu, M. Todd, and S. K. Nam, “Approximate computing: A survey,” IEEE Design Test, vol. 33, no. 1, pp. 8–22, Feb. 2016. [2] S. Mittal, “A survey of techniques for approximate computing,” ACM Comput. Surv., vol. 48, no. 4, pp. 1–33, 2016. [3] S. Venkataramani, S. T. Chakradhar, K. Roy, and A. Raghunathan, “Approximate computing and the quest for computing efficiency,” in Proc. 52nd Annu. Design Autom. Conf., Jun. 2015, pp. 1–6. [4] W. Liu, F. Lombardi, and M. Schulte, “A retrospective and prospective view of approximate computing,” Proc. IEEE, vol. 108, no. 3, pp. 394–399, Mar. 2020. [5] C. S. Lent and P. D. Tougaw, “A device architecture for computing with quantum dots,” Proc. IEEE, vol. 85, no. 4, pp. 541–557, Apr. 1997. [6] M. Vacca et al., “Nanomagnet logic: An architectural level overview,” in Field-Coupled Nanocomputing. Cham, Switzerland: Springer, 2014, pp. 223–256. [7] A. Khitun and K. L. Wang, “Nano scale computational architectures with spin wave bus,” Superlattices Microstruct., vol. 38, no. 3, pp. 184–200, 2005. [8] W. Liu, L. Qian, C. Wang, H. Jiang, J. Han, and F. Lombardi, “Design of approximate radix-4 booth multipliers for error-tolerant computing,” IEEE Trans. Comput., vol. 66, no. 8, pp. 1435–1441, Aug. 2017. [9] Z. Yang, A. Jain, J. Liang, J. Han, and F. Lombardi, “Approximate XOR/XNOR-based adders for inexact computing,” in Proc. 13th IEEE Int. Conf. Nanotechnol. (IEEE-NANO), Aug. 2013, pp. 690–693. [10] H. R. Mahdiani, A. Ahmadi, S. M. Fakhraie, and C. Lucas, “Bio-inspired imprecise computational blocks for efficient VLSI implementation of soft-computing applications,” IEEE Trans. Circuits Syst. I, Reg. Papers, vol. 57, no. 4, pp. 850–862, Apr. 2010. [11] N. Zhu, W. L. Goh, G. Wang, and K. S. Yeo, “Enhanced low-power high-speed adder for error-tolerant application,” in Proc. Int. SoC Design Conf., Nov. 2010, pp. 323–327. [12] S. K. Patel, B. Garg, and S. K. Rai, “An efficient accuracy reconfigurable CLA adder designs using complementary logic,” J. Electron. Test., vol. 36, no. 1, pp. 135–142, Feb. 2020. [13] A. Dalloo, A. Najafi, and A. Garcia-Ortiz, “Systematic design of an approximate adder: The optimized lower part constant-OR adder,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 26, no. 8, pp. 1595–1599, Aug. 2018. [14] F. Frustaci, S. Perri, P. Corsonello, and M. Alioto, “Energy-quality scalable adders based on nonzeroing bit truncation,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 27, no. 4, pp. 964–968, Apr. 2019. [15] W. Liu, T. Zhang, E. McLarnon, M. OrNeill, P. Montuschi, and F. Lombardi, “Design and analysis of majority logic-based approximate adders and multipliers,” IEEE Trans. Emerg. Topics Comput., vol. 9, no. 3, pp. 1609–1624, Jul. 2021. [16] S. Perri, F. Spagnolo, F. Frustaci, and P. Corsonello, “Accuracy improved low-energy multi-bit approximate adders in QCA,” IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 68, no. 11, pp. 3456–3460, Nov. 2021. [17] M. H. Moaiyeri, F. Sabetzadeh, and S. Angizi, “An efficient majoritybased compressor for approximate computing in the nano era,” Microsyst. Technol., vol. 24, no. 3, pp. 1589–1601, Mar. 2018. [18] S. Angizi, H. Jiang, R. F. DeMara, J. Han, and D. Fan, “Majoritybased spin-CMOS primitives for approximate computing,” IEEE Trans. Nanotechnol., vol. 17, no. 4, pp. 795–806, Jul. 2018. [19] M. Taheri, A. Arasteh, S. Mohammadyan, A. Panahi, and K. Navi, “A novel majority based imprecise 4:2 compressor with respect to the current and future VLSI industry,” Microprocessors Microsyst., vol. 73, Mar. 2020, Art. no. 102962. [20] F. Sabetzadeh, M. H. Moaiyeri, and M. Ahmadinejad, “A majoritybased imprecise multiplier for ultra-efficient approximate image multiplication,” IEEE Trans. Circuits Syst. I, Reg. Papers, vol. 66, no. 11, pp. 4200–4208, Nov. 2019. [21] F. Salmanpour, M. H. Moaiyeri, and F. Sabetzadeh, “Ultra-compact imprecise 4:2 compressor and multiplier circuits for approximate computing in deep nanoscale,” Circuits, Syst., Signal Process., vol. 40, no. 9, pp. 4633–4650, Sep. 2021. [22] F. S. Torres, R. Wille, P. Niemann, and R. Drechsler, “An energy-aware model for the logic synthesis of quantum-dot cellular automata,” IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., vol. 37, no. 12, pp. 3031–3041, Dec. 2018. [23] L. Amarú, P.-E. Gaillardon, and G. De Micheli, “Majority-inverter graph: A novel data-structure and algorithms for efficient logic optimization,” in Proc. 51st Annu. Design Autom. Conf. Design Autom. Conf. (DAC), 2014, pp. 1–6. [24] W. Haaswijk, M. Soeken, L. Amarú, P.-E. Gaillardon, and G. D. Micheli, “A novel basis for logic rewriting,” in Proc. 22nd Asia South Pacific Design Autom. Conf. (ASP-DAC), Jan. 2017, pp. 151–156. [25] L. Amaru, P. E. Gaillardon, and G. D. Micheli, “Majority-inverter graph: A new paradigm for logic optimization,” IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., vol. 35, no. 5, pp. 806–819, May 2016. [26] Z. Chu, M. Soeken, Y. Xia, L. Wang, and G. D. Micheli, “Advanced functional decomposition using majority and its applications,” IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., vol. 39, no. 8, pp. 1621–1634, Aug. 2020. [27] Z. Chu, Z. Li, Y. Xia, L. Wang, and W. Liu, “BCD adder designs based on three-input XOR and majority gates,” IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 68, no. 6, pp. 1942–1946, Jun. 2021. [28] Z. Chu, H. Tian, Z. Li, Y. Xia, and L. Wang, “A high-performance design of generalized pipeline cellular array,” IEEE Comput. Archit. Lett., vol. 19, no. 1, pp. 47–50, Jan. 2020. [29] M. Soeken, L. G. Amaru, P.-E. Gaillardon, and G. D. Micheli, “Exact synthesis of majority-inverter graphs and its applications,” IEEE Trans. Comput.-Aided Design Integr. Circuits Syst., vol. 36, no. 11, pp. 1842–1855, Nov. 2017. [30] H. Cho and E. E. Swartzlander, “Adder and multiplier design in quantum-dot cellular automata,” IEEE Trans. Comput., vol. 58, no. 6, pp. 721–727, Jun. 2009. [31] C.-H. Chang, J. Gu, and M. Zhang, “Ultra low-voltage low-power CMOS 4–2 and 5–2 compressors for fast arithmetic circuits,” IEEE Trans. [32] J. Liang, J. Han, and F. Lombardi, “New metrics for the reliability of approximate and probabilistic adders,” IEEE Trans. Comput., vol. 62, no. 9, pp. 1760–1771, Sep. 2013. [33] C. Labrado, H. Thapliyal, and F. Lombardi, “Design of majority logic based approximate arithmetic circuits,” in Proc. IEEE Int. Symp. Circuits Syst. (ISCAS), May 2017, pp. 1–4. [34] T. Zhang, W. Liu, E. McLarnon, M. O’Neill, and F. Lombardi, “Design of majority logic (ML) based approximate full adders,” in Proc. IEEE Int. Symp. Circuits Syst. (ISCAS), May 2018, pp. 1–5. [35] V. Pudi and K. Sridharan, “Low complexity design of ripple carry and Brent–Kung adders in QCA,” IEEE Trans. Nanotechnol., vol. 11, no. 1, pp. 105–119, Jan. 2012. [36] A. Hore and D. Ziou, “Image quality metrics: PSNR vs. SSIM,” in Proc. 20th Int. Conf. Pattern Recognit., Aug. 2010, pp. 2366–2369. [37] J. Choi, Z. Wang, S. Venkataramani, P. I-Jen Chuang, V. Srinivasan, and K. Gopalakrishnan, “PACT: Parameterized clipping activation for quantized neural networks,” 2018, arXiv:1805.06085. [38] P. J. Song and G. De Micheli, “Circuit and architecture trade-offs for high-speed multiplication,” IEEE J. Solid-State Circuits, vol. 26, no. 9, pp. 1184–1198, Sep. 1991. [39] A. Momeni, J. Han, P. Montuschi, and F. Lombardi, “Design and analysis of approximate compressors for multiplication,” IEEE Trans. Comput., vol. 64, no. 4, pp. 984–994, Apr. 2015. [40] S.-W. Kim and E. E. Swartzlander, “Multipliers with coplanar crossings for quantum-dot cellular automata,” in Proc. 10th IEEE Int. Conf. Nanotechnol., Aug. 2010, pp. 953–957. [41] S.-W. Kim and E. E. Swartzlander, “Parallel multipliers for quantum-dot cellular automata,” in Proc. IEEE Nanotechnol. Mater. Devices Conf., Jun. 2009, pp. 68–72. [42] B. Jacob et al., “Quantization and training of neural networks for efficient integer-arithmetic-only inference,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Jun. 2018, pp. 2704–2713. [43] Y. Qian, C. Meng, Y. Zhang, W. Qian, R. Wang, and R. Huang, “Approximate logic synthesis in the loop for designing low-power neural network accelerator,” in Proc. IEEE Int. Symp. Circuits Syst. (ISCAS), May 2021, pp. 1–5. [44] Tiny-DNN. Accessed: Mar. 14, 2022. [Online]. Available: https:// github.com/tiny-dnn/tiny-dnn [45] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” Proc. IEEE, vol. 86, no. 11, pp. 2278–2324, Nov. 1998.

Copyright

Copyright © 2023 Manchiryala Manogna, M. Shiva Kumar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.